PERCUSIÓN EN UNA BOLA DE BILLAR
En este post, se estudia el movimiento de una bola de billar sobre la superficie plana de un paño sometida a un impacto o percusión localizada en un punto del plano vertical que pasa por el centro de la bola. Supondremos que el tiempo de impacto es muy pequeño.
La fuerza de la colisión con el taco determina la velocidad inicial de traslación de la bola. Por otro lado, el taco genera un movimiento que produce una velocidad inicial de rotación alrededor del centro de la bola de billar.
MOVIMIENTO DE LA BOLA CON SOBREGIRO / CORRIDO
En la figura, observamos todas las fuerzas que actúan sobre la bola de billar cuando el taco golpea la bola a una altura h por encima del paño.
La fuerza F que actúa sobre el punto B y forma un ángulo Φ=Ø+Θ con la vertical.
El
peso mg que actúa en el centro de la bola.
La
reacción del plano horizontal que actúa en el punto de contacto A y
vale
NA=mg+FcosΦ
El
rozamiento por deslizamiento en A que vale
RA=µANA
La fuerza
de rozamiento RA se opone a la velocidad en el punto A,
puede estar en el sentido indicado o en sentido contrario según que la
velocidad de A sea negativa o positiva.
La fuerza F
que actúa en B se puede descomponer en otras dos, una componente en la
dirección radial NB y otra en la dirección tangencial RB.
Ambas están relacionadas
RB=µBNB con µB=tanØ
Donde µB es el coeficiente dinámico de
rozamiento entre el taco y la bola, el cual puede ser modificado a voluntad
por el jugador con la tiza.
Conociendo
las fuerzas que actúan sobre la bola y el tiempo τ que actúan sobre la misma podemos
determinar la velocidad inicial de traslación V0 del cuerpo móvil (en adelante c.m.) y
la velocidad inicial de rotación w0. Las ecuaciones del impulso lineal
y del impulso angular se escriben
Donde RB = F·senØ. Vamos a suponer que durante el breve intervalo de tiempo τ que dura el impacto, se puede despreciar el rozamiento RA de la bola con el paño, frente a la componente horizontal F·senΦ de la fuerza que ejerce el taco, con tal que el rozamiento RB del taco y la bola sea suficientemente grande y el golpe no sea demasiado alto h→2r. Bajo estas condiciones las ecuaciones del impulso lineal y angular se convierten en
El impulso de la fuerza F es la cantidad desconocida que eliminamos de ambas ecuaciones. Para una esfera de masa m y radio r, el momento de inercia Ic=2mr2/5. La relación entre las velocidades iniciales de traslación del c.m.V0 y de rotación alrededor de un eje que pasa por el c.m. w0 es
Teniendo en cuenta que µB=tgØ, Φ=Ø +Θ , y que la altura h y el ángulo Θ están relacionados por
La siguiente expresión relaciona las velocidades iniciales de traslación y rotación de la bola de billar
donde hemos puesto ß =cosΘ para simplificar la expresión final.
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Donde RB = F·senØ. Vamos a suponer que durante el breve intervalo de tiempo τ que dura el impacto, se puede despreciar el rozamiento RA de la bola con el paño, frente a la componente horizontal F·senΦ de la fuerza que ejerce el taco, con tal que el rozamiento RB del taco y la bola sea suficientemente grande y el golpe no sea demasiado alto h→2r. Bajo estas condiciones las ecuaciones del impulso lineal y angular se convierten en
El impulso de la fuerza F es la cantidad desconocida que eliminamos de ambas ecuaciones. Para una esfera de masa m y radio r, el momento de inercia Ic=2mr2/5. La relación entre las velocidades iniciales de traslación del c.m.V0 y de rotación alrededor de un eje que pasa por el c.m. w0 es
Teniendo en cuenta que µB=tgØ, Φ=Ø +Θ , y que la altura h y el ángulo Θ están relacionados por
La siguiente expresión relaciona las velocidades iniciales de traslación y rotación de la bola de billar
donde hemos puesto ß =cosΘ para simplificar la expresión final.
La velocidad
inicial del punto de contacto A entre la bola y el paño se puede obtener
sumando la velocidad correspondiente al movimiento de traslación con la
velocidad correspondiente al movimiento de rotación
Esta velocidad es positiva o negativa según que µB sea menor o mayor que el parámetro kβ definido por
Una vez establecidas las condiciones iniciales del movimiento con sobregiro, veamos el movimiento en ausencia de la fuerza F de impacto del taco con la bola.
La fuerza
de rozamiento RA será positiva.
Las ecuaciones del movimiento de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. son:
mac=RA
Ica =-rRA
Esta velocidad es positiva o negativa según que µB sea menor o mayor que el parámetro kβ definido por
Una vez establecidas las condiciones iniciales del movimiento con sobregiro, veamos el movimiento en ausencia de la fuerza F de impacto del taco con la bola.
Consideremos
estos dos casos:
La velocidad inicial del punto de contacto A de la
bola con el tapiz es negativa
Las ecuaciones del movimiento de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. son:
mac=RA
Ica =-rRA
Con NA=mg
y RA=µANA
La velocidad del c.m. crece y la velocidad de rotación decrece
La velocidad del punto de contacto A viene dada por VA=vc-w r y llegará un momento que se anule a partir del cual la bola de billar rodará sin deslizar con velocidad constante.
La velocidad inicial del punto de contacto A de la bola con el tapiz es positiva
La velocidad del c.m. crece y la velocidad de rotación decrece
La velocidad del punto de contacto A viene dada por VA=vc-w r y llegará un momento que se anule a partir del cual la bola de billar rodará sin deslizar con velocidad constante.
La velocidad inicial del punto de contacto A de la bola con el tapiz es positiva
La fuerza
de rozamiento RA será negativa
Como hay dos movimientos uno de rotación y otro de traslación habrá que plantear dos ecuaciones
Como hay dos movimientos uno de rotación y otro de traslación habrá que plantear dos ecuaciones
mac=-RA
Ica =rRA
Con NA=mg
y RA=µANA
La velocidad del c.m. decrece y la velocidad de rotación crece
La velocidad del punto de contacto A viene dada por VA=vc-w r y llegará un momento que se anule a partir del cual la bola de billar rodará sin deslizar con velocidad constante.
Ejemplo
La velocidad del c.m. decrece y la velocidad de rotación crece
La velocidad del punto de contacto A viene dada por VA=vc-w r y llegará un momento que se anule a partir del cual la bola de billar rodará sin deslizar con velocidad constante.
Ejemplo
Como vemos
en las fórmulas la velocidad final de la bola, no depende directamente del
radio de la bola sino de un parámetro adimensional.
Datos fijados en el programa interactivo
Velocidad inicial de A negativa
Datos fijados en el programa interactivo
Velocidad inicial de A negativa
Datos
introducidos por el usuario.
En este
caso ß=0.4 y µB>kb =0.43
Estamos en
el caso que (VA)0 es negativa. El tiempo que
tarda en rodar sin deslizar es de 0.043 s. Y la velocidad final constante del
c.m. es de 1.08 m/s.
Velocidad
inicial de A positiva
Datos
introducidos por el usuario.
La reacción del paño en A es:
Para impactos grandes se puede hacer que la bola abandone el paño. En lo sucesivo supondremos que NA es positivo, y que este caso no sucede.
La velocidad en el punto de contacto A de la bola con el paño es siempre positiva
Aplicando las ecuaciones del impulso lineal y del impulso angular y suponiendo que la fuerza de rozamiento RA es pequeño frente a la componente horizontal de la fuerza de impacto durante el breve periodo t que dura el contacto del taco con la bola, obtenemos la relación entre la velocidad inicial del c.m. y la velocidad angular inicial de rotación alrededor de un eje que pasa por el c.m.
y a continuación, la velocidad inicial del punto de contacto A de la bola con el paño
ahora el parámetro ß vale
ya que h es menor que r.
Se anula la velocidad angular
Las ecuaciones del movimiento de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. son:
Con NA=mg
y RA=µANA
La velocidad del c.m. decrece y la velocidad de rotación también decrece
Aquí surgen dos posibilidades que vc se anule antes que w o bien, que w se anule antes que vc. Normalmente, se anula w antes que vc de modo que la bola no retrocede.
en dicho instante la velocidad del c.m. es
Se establece el movimiento de rodar sin deslizar
En el
momento en que se anula la velocidad angular de rotación, la velocidad del
centro de masas y la velocidad del punto de contacto A de la bola con el
tapiz se igualan. A partir de ese instante, la fricción RA
entre la bola y el paño hace que aparezca una velocidad angular de rotación.
Las ecuaciones del movimiento de traslación y de rotación son:
En este
caso ß=0.4 y µB<kb =0.43
Estamos en
el caso que (VA)0 es positiva. El tiempo que
tarda en rodar sin deslizar es de 0.040 s. Y la velocidad final constante del
c.m. es de 0.92 m/s.
MOVIMIENTO DE LA BOLA CON CONTRAGIRO / RETROCESO
El planteamiento es similar al movimiento de la bola con sobregiro. Sin embargo, hay algunas diferencias
MOVIMIENTO DE LA BOLA CON CONTRAGIRO / RETROCESO
El planteamiento es similar al movimiento de la bola con sobregiro. Sin embargo, hay algunas diferencias
La reacción del paño en A es:
NA=mg-FcosФ
Con Φ =Ø +Θ
Con Φ =Ø +Θ
Para impactos grandes se puede hacer que la bola abandone el paño. En lo sucesivo supondremos que NA es positivo, y que este caso no sucede.
La velocidad en el punto de contacto A de la bola con el paño es siempre positiva
Aplicando las ecuaciones del impulso lineal y del impulso angular y suponiendo que la fuerza de rozamiento RA es pequeño frente a la componente horizontal de la fuerza de impacto durante el breve periodo t que dura el contacto del taco con la bola, obtenemos la relación entre la velocidad inicial del c.m. y la velocidad angular inicial de rotación alrededor de un eje que pasa por el c.m.
y a continuación, la velocidad inicial del punto de contacto A de la bola con el paño
ahora el parámetro ß vale
ya que h es menor que r.
Estas
ecuaciones son válidas salvo en el caso de que el golpe sea muy bajo h→0.
Una vez
establecidas las condiciones iniciales del movimiento con contragiro, veamos
el movimiento en ausencia de la fuerza F de impacto del taco con la
bola.
Las ecuaciones del movimiento de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. son:
mac=-RA
Ica =-rRA
Ica =-rRA
Con NA=mg
y RA=µANA
La velocidad del c.m. decrece y la velocidad de rotación también decrece
Aquí surgen dos posibilidades que vc se anule antes que w o bien, que w se anule antes que vc. Normalmente, se anula w antes que vc de modo que la bola no retrocede.
La
velocidad angular se hace cero w=0 en el instante
en dicho instante la velocidad del c.m. es
Se establece el movimiento de rodar sin deslizar
Las ecuaciones del movimiento de traslación y de rotación son:
mac=-RA
Ica =rRA
Para t>t1 las velocidades de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. serán, respectivamente
Como vc disminuye y w aumenta llegará un momento en el que la velocidad del punto de contacto A, VA=vc-w r se anule, en dicho instante la bola comienza a rodar sin deslizar con velocidad constante
Ejemplo
La fórmula de la velocidad final de la bola, no depende directamente del radio r de la bola sino de un parámetro adimensional
Datos fijados en el programa interactivo
Datos introducidos por el usuario.
Cuando el taco impacta en posición h=r, la fuerza F que actúa sobre la bola es horizontal.
De nuevo suponemos que la fuerza de rozamiento RA es despreciable frente a la fuerza F que actúa sobre la bola.
El momento de dicha fuerza F respecto del c.m. es cero, por tanto la bola no tiene velocidad angular inicial.
De la ecuación del impulso lineal obtendríamos la velocidad V0 del c.m. de la bola si conociéramos la fuerza F y el tiempo t que actúa sobre la misma.
La bola se mueve con una velocidad inicial de traslación V0, la fuerza de rozamiento en el punto de contacto entre la bola y el paño hace que esta gire y por tanto disminuya la velocidad en el punto de contacto A de la bola con el paño.
Las ecuaciones del movimiento de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. son:
Ejemplo
Revista Española de Física. V-3, nº 1, 1989, págs. 31-41
Ica =rRA
Para t>t1 las velocidades de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. serán, respectivamente
Como vc disminuye y w aumenta llegará un momento en el que la velocidad del punto de contacto A, VA=vc-w r se anule, en dicho instante la bola comienza a rodar sin deslizar con velocidad constante
Ejemplo
La fórmula de la velocidad final de la bola, no depende directamente del radio r de la bola sino de un parámetro adimensional
Datos fijados en el programa interactivo
Datos introducidos por el usuario.
En este
caso ß =0.6
La
velocidad angular de rotación se hace cero en el instante 0.156 s. La
velocidad de traslación es de 0.69 m/s.
Luego,
vuelve a incrementarse la velocidad angular de rotación (pero en sentido
contrario) hasta que la velocidad del punto A de contacto de la bola con el tapiz
se hace cero y la bola rueda sin deslizar.
El tiempo
total que transcurre es de 0.257 s y el c.m. alcanza una velocidad constante
de 0.50 m/s.
IMPACTO EN EL CENTRO DE LA BOLA
IMPACTO EN EL CENTRO DE LA BOLA
Cuando el taco impacta en posición h=r, la fuerza F que actúa sobre la bola es horizontal.
De nuevo suponemos que la fuerza de rozamiento RA es despreciable frente a la fuerza F que actúa sobre la bola.
El momento de dicha fuerza F respecto del c.m. es cero, por tanto la bola no tiene velocidad angular inicial.
De la ecuación del impulso lineal obtendríamos la velocidad V0 del c.m. de la bola si conociéramos la fuerza F y el tiempo t que actúa sobre la misma.
La bola se mueve con una velocidad inicial de traslación V0, la fuerza de rozamiento en el punto de contacto entre la bola y el paño hace que esta gire y por tanto disminuya la velocidad en el punto de contacto A de la bola con el paño.
Las ecuaciones del movimiento de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m. son:
mac=-RA
Ica =rRA
Ica =rRA
Con NA=mg
y RA=µANA
La velocidad del c.m. disminuye y la velocidad angular de rotación aumenta.
Al cabo de un cierto tiempo t, la velocidad del punto A se hace cero, y la bola rueda sin deslizar con velocidad constante.
vA es cero en el instante
En dicho instante la velocidad constante del c.m. es
y RA=µANA
La velocidad del c.m. disminuye y la velocidad angular de rotación aumenta.
Al cabo de un cierto tiempo t, la velocidad del punto A se hace cero, y la bola rueda sin deslizar con velocidad constante.
vA es cero en el instante
En dicho instante la velocidad constante del c.m. es
Ejemplo
Datos
fijados en el programa interactivo
Datos introducidos por el usuario
- Coeficiente de rozamiento (Taco-bola) µß, actuando en la barra de desplazamiento llamada coeficiente de rozamiento.
- La altura del taco sobre el suelo h, actuando en la barra de desplazamiento llamada Altura.
- El radio de la esfera se ha fijado en r=5 mm
- La velocidad inicial de traslación del c.m. en V0=1 m/s
- El coeficiente de rozamiento (bola-paño) µA=0.2
Datos introducidos por el usuario
La
velocidad del punto de contacto A de la bola con el suelo se hace cero en el
instante t=0.145 s. A partir de este instante, la bola rueda sin
deslizar con velocidad constante vc=0.71 m/s.
ACTIVIDADES
Se introduce:
ACTIVIDADES
Se introduce:
- Coeficiente de rozamiento (Taco-bola) µß, actuando en la barra de desplazamiento llamada coeficiente de rozamiento.
- La altura del taco sobre el suelo h, actuando en la barra de desplazamiento llamada Altura.
- El radio de la esfera se ha fijado en r=5 mm
- La velocidad inicial de traslación del c.m. en V0=1 m/s
- El coeficiente de rozamiento (bola-paño) µA=0.2
Observar
el movimiento de traslación del c.m. y de rotación alrededor de un eje que
pasa por el c.m. de la bola de billar.
Una flecha
nos muestra la velocidad del punto de contacto de la bola de billar con el paño.
Cuando la velocidad de este punto es cero, la bola de billar rueda
sin deslizar con velocidad constante.
REFERENCIAS
Jiménez F. Mecánica del billar I: Movimiento de la bola sobre el paño.
REFERENCIAS
Jiménez F. Mecánica del billar I: Movimiento de la bola sobre el paño.
Revista Española de Física. V-3, nº 1, 1989, págs. 31-41
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
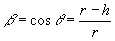
0 comentarios:
Publicar un comentario